Quantum Machine Learning and the Power of Data
June 22, 2021
Quantum computing has rapidly advanced in both theory and practice in recent years, and with it the hope for the potential impact in real applications. One key area of interest is how quantum computers might affect machine learning. We recently demonstrated experimentally that quantum computers are able to naturally solve certain problems with complex correlations between inputs that can be incredibly hard for traditional, or “classical”, computers. This suggests that learning models made on quantum computers may be dramatically more powerful for select applications, potentially boasting faster computation, better generalization on less data, or both. Hence it is of great interest to understand in what situations such a “quantum advantage” might be achieved.
The idea of quantum advantage is typically phrased in terms of computational advantages. That is, given some task with well defined inputs and outputs, can a quantum computer achieve a more accurate result than a classical machine in a comparable runtime? There are a number of algorithms for which quantum computers are suspected to have overwhelming advantages, such as Shor’s factoring algorithm for factoring products of large primes (relevant to RSA encryption) or the quantum simulation of quantum systems. However, the difficulty of solving a problem, and hence the potential advantage for a quantum computer, can be greatly impacted by the availability of data. As such, understanding when a quantum computer can help in a machine learning task depends not only on the task, but also the data available, and a complete understanding of this must include both.
In “Power of data in quantum machine learning”, published in Nature Communications, we dissect the problem of quantum advantage in machine learning to better understand when it will apply. We show how the complexity of a problem formally changes with the availability of data, and how this sometimes has the power to elevate classical learning models to be competitive with quantum algorithms. We then develop a practical method for screening when there may be a quantum advantage for a chosen set of data embeddings in the context of kernel methods. We use the insights from the screening method and learning bounds to introduce a novel method that projects select aspects of feature maps from a quantum computer back into classical space. This enables us to imbue the quantum approach with additional insights from classical machine learning that shows the best empirical separation in quantum learning advantages to date.
Computational Power of Data
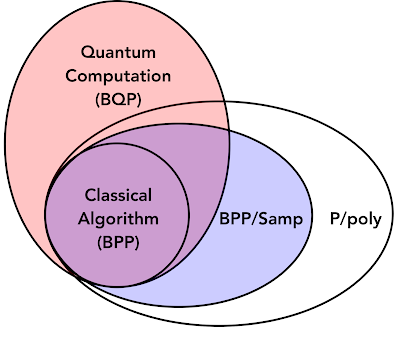
The idea of quantum advantage over a classical computer is often framed in terms of computational complexity classes. Examples such as factoring large numbers and simulating quantum systems are classified as bounded quantum polynomial time (BQP) problems, which are those thought to be handled more easily by quantum computers than by classical systems. Problems easily solved on classical computers are called bounded probabilistic polynomial (BPP) problems.
We show that learning algorithms equipped with data from a quantum process, such as a natural process like fusion or chemical reactions, form a new class of problems (which we call BPP/Samp) that can efficiently perform some tasks that traditional algorithms without data cannot, and is a subclass of the problems efficiently solvable with polynomial sized advice (P/poly). This demonstrates that for some machine learning tasks, understanding the quantum advantage requires examination of available data as well.
Geometric Test for Quantum Learning Advantage
Informed by the results that the potential for advantage changes depending on the availability of data, one may ask how a practitioner can quickly evaluate if their problem may be well suited for a quantum computer. To help with this, we developed a workflow for assessing the potential for advantage within a kernel learning framework. We examined a number of tests, the most powerful and informative of which was a novel geometric test we developed.
In quantum machine learning methods, such as quantum neural networks or quantum kernel methods, a quantum program is often divided into two parts, a quantum embedding of the data (an embedding map for the feature space using a quantum computer), and the evaluation of a function applied to the data embedding. In the context of quantum computing, quantum kernel methods make use of traditional kernel methods, but use the quantum computer to evaluate part or all of the kernel on the quantum embedding, which has a different geometry than a classical embedding. It was conjectured that a quantum advantage might arise from the quantum embedding, which might be much better suited to a particular problem than any accessible classical geometry.
We developed a quick and rigorous test that can be used to quickly compare a particular quantum embedding, kernel, and data set to a range of classical kernels and assess if there is any opportunity for quantum advantage across, e.g., possible label functions such as those used for image recognition tasks. We define a geometric constant g, which quantifies the amount of data that could theoretically close that gap, based on the geometric test. This is an extremely useful technique for deciding, based on data constraints, if a quantum solution is right for the given problem.
Projected Quantum Kernel Approach
One insight revealed by the geometric test, was that existing quantum kernels often suffered from a geometry that was easy to best classically because they encouraged memorization, instead of understanding. This inspired us to develop a projected quantum kernel, in which the quantum embedding is projected back to a classical representation. While this representation is still hard to compute with a classical computer directly, it comes with a number of practical advantages in comparison to staying in the quantum space entirely.
 |
| Geometric quantity g, which quantifies the potential for quantum advantage, depicted for several embeddings, including the projected quantum kernel introduced here. |
By selectly projecting back to classical space, we can retain aspects of the quantum geometry that are still hard to simulate classically, but now it is much easier to develop distance functions, and hence kernels, that are better behaved with respect to modest changes in the input than was the original quantum kernel. In addition the projected quantum kernel facilitates better integration with powerful non-linear kernels (like a squared exponential) that have been developed classically, which is much more challenging to do in the native quantum space.
This projected quantum kernel has a number of benefits over previous approaches, including an improved ability to describe non-linear functions of the existing embedding, a reduction in the resources needed to process the kernel from quadratic to linear with the number of data points, and the ability to generalize better at larger sizes. The kernel also helps to expand the geometric g, which helps to ensure the greatest potential for quantum advantage.
Data Sets Exhibit Learning Advantages
The geometric test quantifies potential advantage for all possible label functions, however in practice we are most often interested in specific label functions. Using learning theoretic approaches, we also bound the generalization error for specific tasks, including those which are definitively quantum in origin. As the advantage of a quantum computer relies on its ability to use many qubits simultaneously but previous approaches scale poorly in number of qubits, it is important to verify the tasks at reasonably large qubit sizes ( > 20 ) to ensure a method has the potential to scale to real problems. For our studies we verified up to 30 qubits, which was enabled by the open source tool, TensorFlow-Quantum, enabling scaling to petaflops of compute.
Interestingly, we showed that many naturally quantum problems, even up to 30 qubits, were readily handled by classical learning methods when sufficient data were provided. Hence one conclusion is that even for some problems that look quantum, classical machine learning methods empowered by data can match the power of quantum computers. However, using the geometric construction in combination with the projected quantum kernel, we were able to construct a data set that exhibited an empirical learning advantage for a quantum model over a classical one. Thus, while it remains an open question to find such data sets in natural problems, we were able to show the existence of label functions where this can be the case. Although this problem was engineered and a quantum computational advantage would require the embeddings to be larger and more challenging, this work represents an important step in understanding the role data plays in quantum machine learning.
For this problem, we scaled up the number of qubits (n) and compared the prediction accuracy of the projected quantum kernel to existing kernel approaches and the best classical machine learning model in our dataset. Moreover, a key takeaway from these results is that although we showed the existence of datasets where a quantum computer has an advantage, for many quantum problems, classical learning methods were still the best approach. Understanding how data can affect a given problem is a key factor to consider when discussing quantum advantage in learning problems, unlike traditional computation problems for which that is not a consideration.
Conclusions
When considering the ability of quantum computers to aid in machine learning, we have shown that the availability of data fundamentally changes the question. In our work, we develop a practical set of tools for examining these questions, and use them to develop a new projected quantum kernel method that has a number of advantages over existing approaches. We build towards the largest numerical demonstration to date, 30 qubits, of potential learning advantages for quantum embeddings. While a complete computational advantage on a real world application remains to be seen, this work helps set the foundation for the path forward. We encourage any interested readers to check out both the paper and related TensorFlow-Quantum tutorials that make it easy to build on this work.
Acknowledgements
We would like to acknowledge our co-authors on this paper — Michael Broughton, Masoud Mohseni, Ryan Babbush, Sergio Boixo, and Hartmut Neven, as well as the entirety of the Google Quantum AI team. In addition, we acknowledge valuable help and feedback from Richard Kueng, John Platt, John Preskill, Thomas Vidick, Nathan Wiebe, Chun-Ju Wu, and Balint Pato.
1Current affiliation — Institute for Quantum Information and Matter and Department of Computing and Mathematical Sciences, Caltech, Pasadena, CA, USA↩

