Exploring Quantum Neural Networks
December 17, 2018
Posted by Jarrod McClean, Senior Research Scientist and Hartmut Neven, Director of Engineering, Google AI Quantum Team
Since its inception, the Google AI Quantum team has pushed to understand the role of quantum computing in machine learning. The existence of algorithms with provable advantages for global optimization suggest that quantum computers may be useful for training existing models within machine learning more quickly, and we are building experimental quantum computers to investigate how intricate quantum systems can carry out these computations. While this may prove invaluable, it does not yet touch on the tantalizing idea that quantum computers might be able to provide a way to learn more about complex patterns in physical systems that conventional computers cannot in any reasonable amount of time.
Today we talk about two recent papers from the Google AI Quantum team that make progress towards understanding the power of quantum computers for learning tasks. The first constructs a quantum model of neural networks to investigate how a popular classification task might be carried out on quantum processors. In the second paper, we show how peculiar features of quantum geometry change the strategies for training these networks in comparison to their classical counterparts, and offer guidance towards more robust training of these networks.
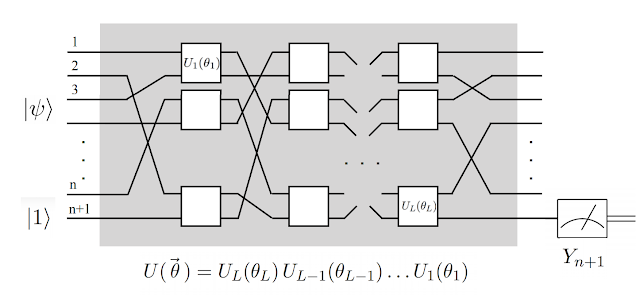
In “Classification with Quantum Neural Networks on Near Term Processors”, we construct a model of quantum neural networks (QNNs) that is specifically designed to work on quantum processors that are expected to be available in the near term. While the current work is primarily theoretical, their structure facilitates implementation and testing on quantum computers in the immediate future. These QNNs can be adapted through supervised learning of labeled data, and we show that it is possible to train a QNN to classify images in the famous MNIST dataset. Follow up work in this area with larger quantum devices may pit the ability of quantum networks to learn patterns against popular classical networks.
Barren Plateaus in Quantum Neural Network Training Landscapes”, we focus on the training of quantum neural networks, and probe questions related to a key difficulty in classical neural networks, which is the problem of vanishing or exploding gradients. In conventional neural networks, a good unbiased initial guess for the neuron weights often involves randomization, although there can be some difficulties as well. Our paper shows that peculiar features of quantum geometry unequivocally prevent this from being a good strategy in the quantum case, instead taking you to barren plateaus. The implications of this work may guide future strategies for initializing and training quantum neural networks.
-
Labels:
- Machine Intelligence
- Quantum