Blog
The latest news from Google AI
Introducing TensorNetwork, an Open Source Library for Efficient Tensor Calculations
Tuesday, June 4, 2019
Posted by Chase Roberts, Research Engineer, Google AI and Stefan Leichenauer, Research Scientist, X
Many of the world's toughest scientific challenges, like developing
high-temperature superconductors
and understanding the
true nature of space and time
, involve dealing with the complexity of quantum systems. What makes these challenges difficult is that the number of
quantum states
in these systems is exponentially large, making brute-force computation infeasible. To deal with this, data structures called
tensor networks
are used. Tensor networks let one focus on the quantum states that are most relevant for real-world problems—the states of low energy, say—while ignoring other states that aren't relevant. Tensor networks are also increasingly finding applications in machine learning (ML). However, there remain difficulties that prohibit them from widespread use in the ML community: 1) a production-level tensor network library for
accelerated hardware
has not been available to run tensor network algorithms at scale, and 2) most of the tensor network literature is geared toward physics applications and creates the false impression that expertise in quantum mechanics is required to understand the algorithms.
In order to address these issues, we are releasing
TensorNetwork
, a brand new open source library to improve the efficiency of tensor calculations, developed in collaboration with the
Perimeter Institute for Theoretical Physics
and
X
. TensorNetwork uses
TensorFlow
as a backend and is optimized for
GPU
processing, which can enable speedups of up to 100x when compared to work on a CPU. We introduce TensorNetwork in a series of papers, the
first
of which presents the new library and its
API
, and provides an overview of tensor networks for a non-physics audience. In our
second paper
we focus on a particular use case in physics, demonstrating the speedup that one gets using GPUs.
How are Tensor Networks Useful?
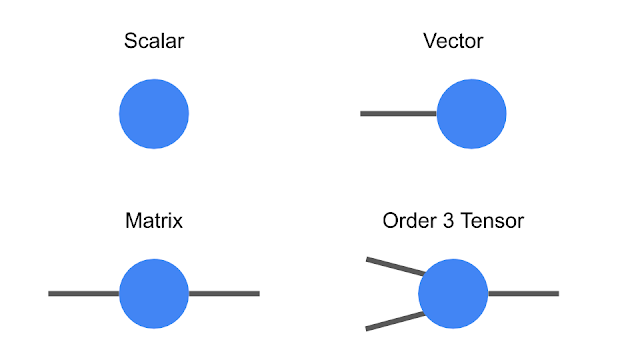
Tensors
are multidimensional arrays, categorized in a hierarchy according to their
order
: e.g., an ordinary number is a tensor of order zero (also known as a
scalar
), a
vector
is an order-one tensor, a
matrix
is an order-two tensor, and so on. While low-order tensors can easily be represented by an explicit array of numbers or with a mathematical symbol such as T
ijnklm
(where the number of indices represents the order of the tensor), that notation becomes very cumbersome once we start talking about high-order tensors. At that point it’s useful to start using diagrammatic notation, where one simply draws a circle (or some other shape) with a number of lines, or legs, coming out of it—the number of legs being the same as the
order
of the tensor. In this notation, a scalar is just a circle, a vector has a single leg, a matrix has two legs, etc. Each leg of the tensor also has a
dimension
, which is the size of that leg. For example, a vector representing an object’s velocity through space would be a three-dimensional, order-one tensor.
Diagrammatic notation for tensors.
The benefit of representing tensors in this way is to succinctly encode mathematical operations, e.g., multiplying a matrix by a vector to produce another vector, or multiplying two vectors to make a scalar. These are all examples of a more general concept called
tensor contraction
.
Diagrammatic notation for tensor contraction. Vector and matrix multiplication, as well as the
matrix trace
(i.e., the sum of the diagonal elements of a matrix), are all examples.
These are also simple examples of
tensor networks
, which are graphical ways of encoding the pattern of tensor contractions of several constituent tensors to form a new one. Each constituent tensor has an order determined by its own number of legs. Legs that are connected, forming an edge in the diagram, represent contraction, while the number of remaining dangling legs determines the order of the resultant tensor.
Left:
The trace of the product of four matrices, tr(ABCD), which is a scalar. You can see that it has no dangling legs.
Right:
Three order-three tensors being contracted with three legs dangling, resulting in a new order-three tensor.
While these examples are very simple, the tensor networks of interest often represent hundreds of tensors contracted in a variety of ways. Describing such a thing would be very obscure using traditional notation, which is why the
diagrammatic notation
was invented by Roger Penrose in 1971.
Tensor Networks in Practice
Consider a collection of black-and-white images, each of which can be thought of as a list of
N
pixel values. A single pixel of a single image can be
one-hot-encoded
into a two-dimensional vector, and by combining these pixel encodings together we can make a 2
N
-dimensional one-hot encoding of the entire image. We can reshape that high-dimensional vector into an order-
N
tensor, and then add up all of the tensors in our collection of images to get a total tensor
T
i1,i2,...,iN
encapsulating the collection.
This sounds like a very wasteful thing to do: encoding images with about 50 pixels in this way would already take
petabytes
of memory. That’s where tensor networks come in. Rather than storing or manipulating the tensor
T
directly, we instead represent
T
as the contraction of many smaller constituent tensors in the shape of a tensor network. That turns out to be much more efficient. For instance, the popular
matrix product state
(MPS) network would write
T
in terms of
N
much smaller tensors, so that the total number of parameters is only linear in
N
, rather than exponential.
The high-order tensor T is represented in terms of many low-order tensors in a matrix product state tensor network.
It’s not obvious that large tensor networks can be efficiently created or manipulated while consistently avoiding the need for a huge amount of memory. But it turns out that this is possible in many cases, which is why tensor networks have been used extensively in quantum physics and, now, in machine learning.
Stoudenmire and Schwab
used the encoding just described to make an image classification model, demonstrating a new use for tensor networks. The TensorNetwork library is designed to facilitate exactly that kind of work, and our
first
paper describes how the library functions for general tensor network manipulations.
Performance in Physics Use-Cases
TensorNetwork
is a general-purpose library for tensor network algorithms, and so it should prove useful for physicists as well. Approximating quantum states is a typical use-case for tensor networks in physics, and is well-suited to illustrate the capabilities of the TensorNetwork library. In our
second paper
, we describe a
tree tensor network
(TTN) algorithm for approximating the ground state of either a periodic quantum spin chain (1D) or a lattice model on a thin torus (2D), and implement the algorithm using TensorNetwork. We compare the use of CPUs with GPUs and observe significant computational speed-ups, up to a factor of 100, when using a GPU and the TensorNetwork library.
Computational time as a function of the bond dimension, χ. The bond dimension determines the size of the constituent tensors of the tensor network. A larger bond dimension means the tensor network is more powerful, but requires more computational resources to manipulate.
Conclusion and Future Work
These are the first in a series of planned papers to illustrate the power of TensorNetwork in real-world applications. In our next paper we will use TensorNetwork to classify images in the
MNIST
and
Fashion-MNIST
datasets. Future plans include time series analysis on the ML side, and quantum circuit simulation on the physics side. With the open source community, we are also always adding new features to TensorNetwork itself. We hope that TensorNetwork will become a valuable tool for physicists and machine learning practitioners.
Acknowledgements
The TensorNetwork library was developed by Chase Roberts, Adam Zalcman, and Bruce Fontaine of Google AI; Ashley Milsted, Martin Ganahl, and Guifre Vidal of the Perimeter Institute; and Jack Hidary and Stefan Leichenauer of X. We’d also like to thank Stavros Efthymiou at X for valuable contributions.
Labels
2018
accessibility
ACL
ACM
Acoustic Modeling
Adaptive Data Analysis
ads
adsense
adwords
Africa
AI
AI for Social Good
Algorithms
Android
Android Wear
API
App Engine
App Inventor
April Fools
Art
Audio
Augmented Reality
Australia
Automatic Speech Recognition
AutoML
Awards
BigQuery
Cantonese
Chemistry
China
Chrome
Cloud Computing
Collaboration
Compression
Computational Imaging
Computational Photography
Computer Science
Computer Vision
conference
conferences
Conservation
correlate
Course Builder
crowd-sourcing
CVPR
Data Center
Data Discovery
data science
datasets
Deep Learning
DeepDream
DeepMind
distributed systems
Diversity
Earth Engine
economics
Education
Electronic Commerce and Algorithms
electronics
EMEA
EMNLP
Encryption
entities
Entity Salience
Environment
Europe
Exacycle
Expander
Faculty Institute
Faculty Summit
Flu Trends
Fusion Tables
gamification
Gboard
Gmail
Google Accelerated Science
Google Books
Google Brain
Google Cloud Platform
Google Docs
Google Drive
Google Genomics
Google Maps
Google Photos
Google Play Apps
Google Science Fair
Google Sheets
Google Translate
Google Trips
Google Voice Search
Google+
Government
grants
Graph
Graph Mining
Hardware
HCI
Health
High Dynamic Range Imaging
ICCV
ICLR
ICML
ICSE
Image Annotation
Image Classification
Image Processing
Inbox
India
Information Retrieval
internationalization
Internet of Things
Interspeech
IPython
Journalism
jsm
jsm2011
K-12
Kaggle
KDD
Keyboard Input
Klingon
Korean
Labs
Linear Optimization
localization
Low-Light Photography
Machine Hearing
Machine Intelligence
Machine Learning
Machine Perception
Machine Translation
Magenta
MapReduce
market algorithms
Market Research
Mixed Reality
ML
ML Fairness
MOOC
Moore's Law
Multimodal Learning
NAACL
Natural Language Processing
Natural Language Understanding
Network Management
Networks
Neural Networks
NeurIPS
Nexus
Ngram
NIPS
NLP
On-device Learning
open source
operating systems
Optical Character Recognition
optimization
osdi
osdi10
patents
Peer Review
ph.d. fellowship
PhD Fellowship
PhotoScan
Physics
PiLab
Pixel
Policy
Professional Development
Proposals
Public Data Explorer
publication
Publications
Quantum AI
Quantum Computing
Reinforcement Learning
renewable energy
Research
Research Awards
resource optimization
Robotics
schema.org
Search
search ads
Security and Privacy
Self-Supervised Learning
Semantic Models
Semi-supervised Learning
SIGCOMM
SIGMOD
Site Reliability Engineering
Social Networks
Software
Sound Search
Speech
Speech Recognition
statistics
Structured Data
Style Transfer
Supervised Learning
Systems
TensorBoard
TensorFlow
TPU
Translate
trends
TTS
TV
UI
University Relations
UNIX
Unsupervised Learning
User Experience
video
Video Analysis
Virtual Reality
Vision Research
Visiting Faculty
Visualization
VLDB
Voice Search
Wiki
wikipedia
WWW
Year in Review
YouTube
Archive
2019
Nov
Oct
Sep
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2018
Dec
Nov
Oct
Sep
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2017
Dec
Nov
Oct
Sep
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2016
Dec
Nov
Oct
Sep
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2015
Dec
Nov
Oct
Sep
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2014
Dec
Nov
Oct
Sep
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2013
Dec
Nov
Oct
Sep
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2012
Dec
Oct
Sep
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2011
Dec
Nov
Sep
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2010
Dec
Nov
Oct
Sep
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2009
Dec
Nov
Aug
Jul
Jun
May
Apr
Mar
Feb
Jan
2008
Dec
Nov
Oct
Sep
Jul
May
Apr
Mar
Feb
2007
Oct
Sep
Aug
Jul
Jun
Feb
2006
Dec
Nov
Sep
Aug
Jul
Jun
Apr
Mar
Feb
Feed
Follow @googleai
Give us feedback in our
Product Forums
.
