Improving Sparse Training with RigL
September 16, 2020
Posted by Utku Evci and Pablo Samuel Castro, Research Engineers, Google Research, Montreal
Modern deep neural network architectures are often highly redundant [1, 2, 3], making it possible to remove a significant fraction of connections without harming performance. The sparse neural networks that result have been shown to be more parameter and compute efficient compared to dense networks, and, in many cases, can significantly decrease wall clock inference times.
By far the most popular method for training sparse neural networks is pruning, (dense-to-sparse training) which usually requires first training a dense model, and then “sparsifying” it by cutting out the connections with negligible weights. However, this process has two limitations.
- The size of the largest trainable sparse model is limited by that of the largest trainable dense model. Even if sparse models are more parameter efficient, one cannot use pruning to train models that are larger and more accurate than the largest possible dense models.
- Pruning is inefficient, meaning that large amounts of computation must be performed for parameters that are zero valued or that will be zero during inference. Additionally, it remains unknown if the performance of the current best pruning algorithms are an upper bound on the quality of sparse models.
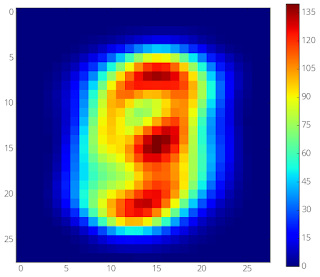
In “Rigging the Lottery: Making All Tickets Winners”, presented at ICML 2020, we introduce RigL, an algorithm for training sparse neural networks that uses a fixed parameter count and computational cost throughout training, without sacrificing accuracy relative to existing dense-to-sparse training methods. The algorithm identifies which neurons should be active during training, which helps the optimization process to utilize the most relevant connections and results in better sparse solutions. An example of this is shown below, where, during the training of a multilayer perceptron (MLP) network on MNIST, our sparse network trained with RigL learns to focus on the center of the images, discarding the uninformative pixels from the edges. A Tensorflow implementation of our method along with three other baselines (SET, SNFS, SNIP) can be found at github.com/google-research/rigl.
 |  |
| Left: Average MNIST image. Right: Evolution of the connectivity of the input throughout the training of a 98% sparse, 2-layer MLP on MNIST. Training starts from a random sparse mask, where each input pixel has roughly six outgoing connections. Connections that originate from the edges do not exhibit meaningful gradients and are therefore replaced by more informative connections that originate from the center pixels. |
RigL Overview
The RigL method starts with a network initialized with a random sparse topology. At regularly spaced intervals we remove a fraction of the connections with the smallest weight magnitudes. Such a strategy has been shown to have very little effect on the loss. RigL then activates new connections using instantaneous gradient information, i.e., without using past gradient information. After updating the connectivity, training continues with the updated network until the next scheduled update. Next, the system activates connections with large gradients, since these connections are expected to decrease the loss most quickly.
Evaluating Performance
By changing the connectivity of the neurons dynamically during training, RigL helps optimize to find better solutions. To demonstrate this, we restart training from a bad solution that exhibits poor accuracy and show that RigL's mask updates help the optimization achieve better loss compared to static training, in which connectivity of the sparse network remains the same.
 |
| Training loss of RigL and Static methods starting from the same static sparse solution, shown together with their final test accuracies. |
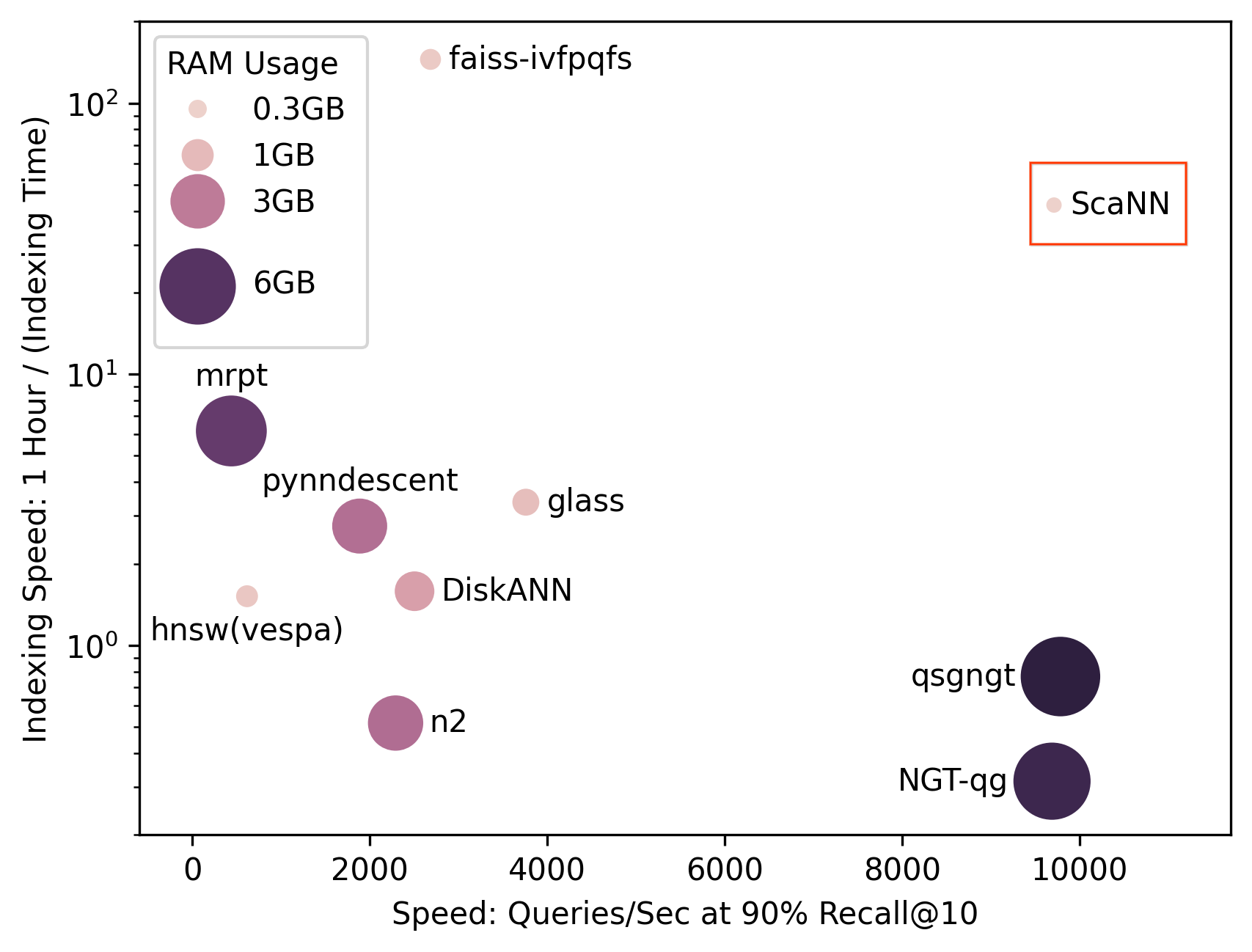
The figure below summarizes the performance of various methods on training an 80% sparse ResNet-50 architecture. We compare RigL with two recent sparse training methods, SET and SNFS and three baseline training methods: Static, Small-Dense and Pruning. Two of these methods (SNFS and Pruning) require dense resources as they need to either train a large network or store the gradients of it. Overall, we observe that the performance of all methods improves with additional training time; thus, for each method we run extended training with up to 5x the training steps of the original 100 epochs.
As noted in a number of studies [4, 5, 6, 7], training a network with fixed sparsity from scratch (Static) leads to inferior performance compared to solutions found by pruning. Training a small, dense network (Small-Dense) with the same number of parameters gets better results than Static, but fails to match the performance of dynamic sparse models. Similarly, SET improves the performance over Small-Dense, but saturates at around 75% accuracy, revealing the limits of growing new connections randomly. Methods that use gradient information to grow new connections (RigL and SNFS) obtain higher accuracy in general, but RigL achieves the highest accuracy, while also consistently requiring fewer FLOPs (and memory footprint) than the other methods.
Observing the trend between extended training and performance, we compare the results using longer training runs. Within the interval considered (i.e., 1x-100x) RigL's performance constantly improves with additional training. RigL achieves state of art performance of 68.07% Top-1 accuracy at training with a 99% sparse ResNet-50 architecture. Similarly extended training of a 90% sparse MobileNet-v1 architecture with RigL achieves 70.55% Top-1 accuracy. Obtaining the same results with fewer training iterations is an exciting future research direction.
 |  |
| Effect of training time on RigL accuracy at training 99% sparse ResNet-50 (left) and 90% sparse MobileNets-v1 (right) architectures. |
Other experiments include image classification on CIFAR-10 datasets and character-based language modelling using RNNs with the WikiText-103 dataset and can be found in the full paper.
Future Work
RigL is useful in three different scenarios:
- Improving the accuracy of sparse models intended for deployment.
- Improving the accuracy of large sparse models that can only be trained for a limited number of iterations.
- Combining with sparse primitives to enable training of extremely large sparse models which otherwise would not be possible.
Acknowledgements We would like to thank Eleni Triantafillou, Hugo Larochelle, Bart van Merrienboer, Fabian Pedregosa, Joan Puigcerver, Danny Tarlow, Nicolas Le Roux, Karen Simonyan for giving feedback on the preprint of the paper; Namhoon Lee for helping us verify and debug our SNIP implementation; Chris Jones for helping us discover and solve the distributed training bug; and Tom Small for creating the visualization of the algorithm.
-
Labels:
- Algorithms & Theory